Aprender a manipular, contar, ordenar em sequência, perceber e fazer movimentos coordenados, desenvolver a memória, resolver operações matemáticas com as mãos é muito significativo para as crianças.Imagem, corpo e conhecimento envolvendo Matemática. Fica a dica e sugestões de atividades.Bom proveito! (Rosangela Vali)



.png)




.png)


Parlendas e Cantigas Matemáticas











A galinha do vizinho
A galinha do vizinho
Bota ovo amarelinha
Bota 1,
Bota 2,
Bota 3,
Bota 4,
Bota 5,
Bota 6,
Bota 7,
Bota 8,
Bota 9,
Bota 10
A galinha do vizinho
Bota ovo amarelinha
Bota 1,
Bota 2,
Bota 3,
Bota 4,
Bota 5,
Bota 6,
Bota 7,
Bota 8,
Bota 9,
Bota 10

PARAFRASEANDO...
UM, maionese de atum,
DOIS, é pra comer depois,
TRÊS, e dar a um gato xadrez.
QUATRO, o sol é um astro,
CINCO, telhado de zinco.
SEIS, festa de reis,
SETE, masca chiclete.
OITO, menino afoito,
NOVE, hoje não chove.
DEZ, arraste os pés,
ONZE, no assoalho de bronze
No Domingo à tarde, a Valéria foi passear com os pais ao seu jardim!Durante o passeio, a Valéria apanhou as tulipas que vês na imagem e algumas rosas.
Quando chegou a casa, enfeitou duas jarras com as tulipas, e depois, colocou uma rosa por cada dezena de tulipas.
Com quantas flores ficou cada jarra?
Durante o passeio, a Valéria apanhou as tulipas que vês na imagem e algumas rosas.
Quando chegou a casa, enfeitou duas jarras com as tulipas, e depois, colocou uma rosa por cada dezena de tulipas.
Com quantas flores ficou cada jarra?
Organização da classe:
- Formar grupos de 3 a 5 participantes;
Capacidades a serem trabalhadas:
Material:
- 10 fichas coloridas (vermelhas, azuis, verdes e brancas) numeradas de 0 a 9;
- Cartaz básico (tamanho A4) com cores variadas
Desenvolvimento:
Organização da classe:
Qual é a sequência?
Matemática com Jogos!
A utilização de atividades lúdicas na Matemática e de materiais concretos é totalmente relacionada ao desenvolvimento cognitivo da criança. Há de se refletir que alguns conteúdos específicos da Matemática não possuem relação com a ideia de serem aplicados utilizando jogos, mas de certa forma promovem um senso crítico, investigador, que ajuda na compreensão e entendimento de determinados tópicos relacionados ao ensino da Matemática.
O nosso aprendiz não pode encarar o jogo como uma parte da aula em que não irá fazer uma atividade escrita ou não precisará prestar atenção no professor, promovendo assim uma conduta de indisciplina e desordem, mas precisa ser conscientizado de que aquele momento é importante para sua formação, pois ele usará de seus conhecimentos e suas experiências para participar, argumentar, propor soluções na busca de chegar aos resultados esperados pelo orientador, porque o jogo pode não ter uma resposta única, mas várias, devemos respeitar as inúmeras respostas, desde que não fujam do propósito.
Selecionei algumas atividades em pesquisa pela NET para construir, aplicar com meus aprendizes e com vocês.Bom proveito!(Rosangela Vali)
STOP DA MATEMÁTICA
Essa é uma ótima sugestão para realizar com os alunos e incentivá-los a estudar tabuada...
Pode ser feita em grupo e cada grupo terá um vencedor, assim os vencedores cuidam para que os outros não continuem escrevendo e isso estimulará o estudo da tabuada, já que os alunos querem vencer.
Você provavelmente conhece o JOGO STOP que fazemos com letras. Na parte de cima, onde especificamos os temas, está colocada a tabuada, e separamos em colunas.
Depois, a cada nova rodada, um número é sorteado, por exemplo o número 8. A partir desse momento, você terá um tempo determinado para multiplicar esse número por cada um da coluna .
O primeiro que preencher as colunas, deverá pedir STOP! e todos os outros não poderão escrever mais nada. Quem preencheu, preencheu.
Agora vamos corrigir as contas com as dos demais jogadores.Nesse caso não se perde ponto já que todos os resultados devem ser iguais, então todos ganham 10 pontos. Se errar perde 5 pontos do que já ganhou!
Somam-se os pontos de cada um na rodada e esses pontos vão para o ranking do STOP!.
Vence quem fizer o maior número de pontos!.
Desafio matemático: as tulipas da Valéria
Quando chegou a casa, enfeitou duas jarras com as tulipas, e depois, colocou uma rosa por cada dezena de tulipas.
Com quantas flores ficou cada jarra?
Durante o passeio, a Valéria apanhou as tulipas que vês na imagem e algumas rosas.
Quando chegou a casa, enfeitou duas jarras com as tulipas, e depois, colocou uma rosa por cada dezena de tulipas.
Com quantas flores ficou cada jarra?
JOGO DAS FICHAS COLORIDAS
- Formar grupos de 3 a 5 participantes;
Capacidades a serem trabalhadas:
- Perceber que o número é formado de algarismos ordenados;
- Relacionar as cores das fichas às ordens numéricas;Material:
- 10 fichas coloridas (vermelhas, azuis, verdes e brancas) numeradas de 0 a 9;
- Cartaz básico (tamanho A4) com cores variadas
Desenvolvimento:
Cada jogador pega uma ficha de cada cor e registra o número formado no quadro somando os valores.
Em seguida passa a vez ao colega. Depois da última jogada ganha aquele que conseguir formar o maior numeral.Este jogo é utilizado para trabalhar o conceito de ordens e classes, podendo ser adaptado para o primeiro e segundo ciclo. O mais importante é a interação.
Os participantes podem ajudar um ao outro, mutuamente, sem interferir no desempenho do vencedor.
O professor deve acompanhar o registro do jogo e fazer as explorações possíveis, graduando as intervenções a cada dia do jogo.
Registro – jogo das fichas coloridas
| |||||
| Aluno(a) | |||||
| Cartas/Jogadas | Vermelha | azul | verde | branca | Número formado |
| 1ª | |||||
| 2ª | |||||
| 3ª | |||||
| 4ª | |||||
| 5ª | |||||
BOTAS DE MUITAS LÉGUAS
Organização da classe:
- Poderá ser realizado com toda a turma, duas equipes ou duplas;
Capacidades a serem trabalhadas:
- Compreender o processo da multiplicação, da divisão e construir fatos básicos;
Material:
- 2 dados;
- Folhas com várias retas numéricas;
Desenvolvimento:
Primeira proposta: Desenhar uma reta numérica no chão.
Um aluno inicia, jogando dois dados diferentes, para representar na reta com passos.
Um aluno inicia, jogando dois dados diferentes, para representar na reta com passos.
O lado do dado maior indicará a quantidade de passos e o lado menor, indicará o tamanho de cada passo.
Outro aluno verifica onde o colega parou para marcar os pontos daquela equipe.
E assim todos farão o mesmo procedimento, disputando quem chegou mais longe.
Segunda proposta: O professor entrega a folha das retas numéricas para as duplas, que jogarão os dados para efetuar as jogadas traçando com o lápis, os passos, seguindo as mesmas regras da primeira
proposta.
proposta.
Ganhará o jogo quem conseguir avançar mais longe na reta numérica.
O professor deverá fazer intervenções para levar o aluno a relacionar as jogadas com a multiplicação e a divisão.
Ex.: 4 passos de 3 distâncias chegará no número 12.
DIAGRAMA DOS HEXÁGONOS
Organização da classe:
- Formar duplas, trio ou individual;
Capacidades a serem trabalhadas:
-Desenvolver coordenação motora fina;
- Construir conceitos de fração, área e perímetro;
- Identificar figuras geométricas;
Material:
- Folha chamex com 4 hexágonos divididos de forma diferente;
- Lápis de cor, tesoura;
Desenvolvimento:
Colorir os hexágonos nas respectivas cores: amarelo, azul, vermelho e verde.
Recortar todas as linhas internas e externas dos mesmos.
A seguir montar um hexágono maior com todas as peças, a partir do amarelo que fica no centro da nova montagem.
É importante que durante a atividade o professor faça as intervenções, levando o aluno a compreender novos conceitos: área, perímetro e fração equivalente.
Exemplos:
1- Quantos triângulos pequenos cabem dentro do novo hexágono?
2- Que fração do novo hexágono, são as peças de cores:
amarela____
azul ___
verde____
vermelho____
3- Quais polígonos você formou quando recortou os hexágonos pequenos?
4- O que você observou no hexágono maior em relação à área de cada cor?
5- o que aconteceu com o perímetro do novo hexágono?
5- o que aconteceu com o perímetro do novo hexágono?
Fonte: Atividades e jogos com números
JOGO DAS POSSIBILIDADES
Organização da classe:
- Formar grupos com 4 a 5 participantes;
Capacidades a serem trabalhadas:
- Trabalhar fatos simples;
- Desenvolver atenção, concentração e raciocínio lógico;
- Explorar conceito intuitivo de probabilidade;
Material:
- 2 dados coloridos;
- Tabuleiro com escudos dos times;
- Quadro de registro das jogadas;
Desenvolvimento:
Cada participante escolhe ou sorteia o time para apostar.
O primeiro jogador lança os dois dados de cores diferentes e observa se
a coluna horizontal e vertical contém o escudo do time que ele escolheu.
a coluna horizontal e vertical contém o escudo do time que ele escolheu.
Se tiver nas duas colunas soma os pontos dos dois dados, se tiver
apenas em uma das colunas, subtrai os números dos dados.
apenas em uma das colunas, subtrai os números dos dados.
Caso não tenha em nenhuma das duas colunas passa a vez para o
colega.
colega.
Cada jogador registra no quadro as jogadas.
Ganha o jogo o participante que obtiver o maior número no total.
Intervenções possíveis:
- Quais os times mais difíceis de sair?
- Como posso obter a pontuação 12?
- Qual o time que tem as mesmas chances de sair?
- Pode-se também substituir os fatos da adição pela multiplicação e da
subtração pela adição
subtração pela adição
REGISTRO – JOGO DAS POSSIBILIDADES / TIMES | ||||||
| Aluno(a) | ||||||
| Jogadas/Times | 1ª jogada | 2ª jogada | 3ª jogada | 4ª jogada | 5ª jogada | Total |
Para visualizar melhor e copiar, clique na imagem para ampliar.
DOMINÓ HUMANO
Pratinho dos fatos ( fixar fatos da multiplicação, adição ou subtração)
Pratinho das ordens
Representação dos Fatos
Operando com varetas
Qual é a sequência?
Descubra o número intruso
Fontes:http://alfabetizacaocefaproponteselacerda.blogspot.com/
http://esqueirinhos.blogs.sapo.pt/2011/03/
http://soatividadesparasaladeaula.blogspot.com/
Marcos Noé-Equipe Brasil Escola
http://esqueirinhos.blogs.sapo.pt/2011/03/
http://soatividadesparasaladeaula.blogspot.com/
Marcos Noé-Equipe Brasil Escola

A palavra discalculia vem do grego (dis, mal) e do Latin (calculare, contar) formando: contando mal. Essa palavra calculare vem, por sua vez, de cálculo, que significa o seixo ou um dos contadores em um ábaco.
A Discalculia é uma desordem neurológica especifica que afeta a habilidade de uma pessoa compreender manipular números
Os transtornos de aprendizagem tais como: a dislexia, a dispraxia, disgrafia, a discalculia é diagnosticada uma deficiência específica na leitura, na escrita e na matemática. Os indivíduos que apresentam um baixo rendimento escolar, lentidão extrema da velocidade de resolução de questões, esperado para seu nível desenvolvimento e escolaridade.
Na área da neuropsicologia as áreas afetadas são:
• Áreas terciárias do hemisfério esquerdo que dificulta a leitura e compreensão dos
problemas verbais, compreensão de conceitos matemáticos;
• Lobos frontais dificultando a realização de cálculos mentais rápidos, habilidade de solução de problemas e conceitualização abstrata.
• Áreas secundárias occípito-parietais esquerdos dificultando a discriminação visual de símbolos matemáticos escritos.
• Lobo temporal esquerdo dificultando memória de séries, realizações matemáticas básicas.
De acordo com Johnson e Myklebust a criança com discalculia é incapaz de:
• Visualizar conjuntos de objetos dentro de um conjunto maior;
• Conservar a quantidade: não compreendem que 1 quilo é igual a quatro pacotes de 250 gramas.
• Sequenciar números: o que vem antes do 11 e depois do 15 – antecessor e sucessor.
• Classificar números.
• Compreender os sinais +, - , ÷, ×.
• Montar operações.
• Entender os princípios de medida.
• Lembrar as sequências dos passos para realizar as operações matemáticas.
• Estabelecer correspondência um a um: não relaciona o número de alunos de uma sala à quantidade de carteiras.
• Contar através dos cardinais e ordinais.
Os processos cognitivos envolvidos na discalculia são:
1. Dificuldade na memória de trabalho;
2. Dificuldade de memória em tarefas não-verbais;
3. Dificuldade na soletração de não-palavras (tarefas de escrita);
4. Não há problemas fonológicos;
5. Dificuldade na memória de trabalho que implica contagem;
6. Dificuldade nas habilidades visuo-espaciais;
7. Dificuldade nas habilidades psicomotoras e perceptivo-táteis.
Quais os comprometimentos?
• Organização espacial.
• Autoestima.
• Orientação temporal.
• Memória.
• Habilidades sociais.
• Habilidades grafomotoras.
• Linguagem/leitura.
• Impulsividade.
• Inconsistência (memorização).
Ajuda do professor / DICAS:
O aluno deve ter um atendimento individualizado por parte do professor que deve evitar:
• Ressaltar as dificuldades do aluno, diferenciando-o dos demais.
• Mostrar impaciência com a dificuldade expressada pelo aluno ou interrompê-lo várias vezes ou mesmo tentar adivinhar o que ele quer dizer completando sua fala.
• Corrigir o aluno frequentemente diante da turma, para não o expor.
• Ignorar a criança em sua dificuldade.
· Não force o aluno a fazer as lições quando estiver nervoso por não ter conseguido.
· Explique a ele suas dificuldades e diga que está ali para ajudá-lo sempre que precisar.
· Proponha jogos na sala.
· Procure usar situações concretas, nos problemas.
Qual a diferença? Acalculia e Discalculia.
A acalculia ocorre quando o indivíduo, após sofrer lesão cerebral, como um acidente vascular cerebral ou um traumatismo crânio-encefálico, perde as habilidades matemáticas já adquiridas. A perda ocorre em níveis variados para realização de cálculos matemáticos.
Cuidado!
As crianças, devido a uma série de fatores, tendem a não gostar da matemática, achar chata, difícil. Verifique se não é uma inadaptação ao ensino da escola, ou ao professor que pode estar causando este mal estar. Se sua criança é saudável e está se desenvolvendo normalmente em outras disciplinas não se desespere, mas é importante procurar um psicopedagogo para uma avaliação.
Muitas confundem inclusive maior-menor, mais-menos, igual-diferente, acarretando erros que poderão ser melhorados com a ajuda de um professor mais atento.
A palavra discalculia vem do grego (dis, mal) e do Latin (calculare, contar) formando: contando mal. Essa palavra calculare vem, por sua vez, de cálculo, que significa o seixo ou um dos contadores em um ábaco.
Na área da neuropsicologia as áreas afetadas são:
• Áreas terciárias do hemisfério esquerdo que dificulta a leitura e compreensão dos
problemas verbais, compreensão de conceitos matemáticos;
• Lobos frontais dificultando a realização de cálculos mentais rápidos, habilidade de solução de problemas e conceitualização abstrata.
• Áreas secundárias occípito-parietais esquerdos dificultando a discriminação visual de símbolos matemáticos escritos.
• Lobo temporal esquerdo dificultando memória de séries, realizações matemáticas básicas.
De acordo com Johnson e Myklebust a criança com discalculia é incapaz de:
• Visualizar conjuntos de objetos dentro de um conjunto maior;
• Conservar a quantidade: não compreendem que 1 quilo é igual a quatro pacotes de 250 gramas.
• Sequenciar números: o que vem antes do 11 e depois do 15 – antecessor e sucessor.
• Classificar números.
• Compreender os sinais +, - , ÷, ×.
• Montar operações.
• Entender os princípios de medida.
• Lembrar as sequências dos passos para realizar as operações matemáticas.
• Estabelecer correspondência um a um: não relaciona o número de alunos de uma sala à quantidade de carteiras.
• Contar através dos cardinais e ordinais.
Os processos cognitivos envolvidos na discalculia são:
1. Dificuldade na memória de trabalho;
2. Dificuldade de memória em tarefas não-verbais;
3. Dificuldade na soletração de não-palavras (tarefas de escrita);
4. Não há problemas fonológicos;
5. Dificuldade na memória de trabalho que implica contagem;
6. Dificuldade nas habilidades visuo-espaciais;
7. Dificuldade nas habilidades psicomotoras e perceptivo-táteis.
Quais os comprometimentos?
• Organização espacial.
• Autoestima.
• Orientação temporal.
• Memória.
• Habilidades sociais.
• Habilidades grafomotoras.
• Linguagem/leitura.
• Impulsividade.
• Inconsistência (memorização).
Ajuda do professor / DICAS:
O aluno deve ter um atendimento individualizado por parte do professor que deve evitar:
• Ressaltar as dificuldades do aluno, diferenciando-o dos demais.
• Mostrar impaciência com a dificuldade expressada pelo aluno ou interrompê-lo várias vezes ou mesmo tentar adivinhar o que ele quer dizer completando sua fala.
• Corrigir o aluno frequentemente diante da turma, para não o expor.
• Ignorar a criança em sua dificuldade.
· Não force o aluno a fazer as lições quando estiver nervoso por não ter conseguido.
· Explique a ele suas dificuldades e diga que está ali para ajudá-lo sempre que precisar.
· Proponha jogos na sala.
· Procure usar situações concretas, nos problemas.
Qual a diferença? Acalculia e Discalculia.
A acalculia ocorre quando o indivíduo, após sofrer lesão cerebral, como um acidente vascular cerebral ou um traumatismo crânio-encefálico, perde as habilidades matemáticas já adquiridas. A perda ocorre em níveis variados para realização de cálculos matemáticos.
Cuidado!
As crianças, devido a uma série de fatores, tendem a não gostar da matemática, achar chata, difícil. Verifique se não é uma inadaptação ao ensino da escola, ou ao professor que pode estar causando este mal estar. Se sua criança é saudável e está se desenvolvendo normalmente em outras disciplinas não se desespere, mas é importante procurar um psicopedagogo para uma avaliação.
Muitas confundem inclusive maior-menor, mais-menos, igual-diferente, acarretando erros que poderão ser melhorados com a ajuda de um professor mais atento.
Minhas Sugestões:
Já foram aplicadas por mim, na prática, como professora e psicopedagoga. Trouxeram significativa evolução de rendimento na matemática por trabalharem a atenção, concentração,sequência, ritmo, organização espacial, temporal.
Já foram aplicadas por mim, na prática, como professora e psicopedagoga. Trouxeram significativa evolução de rendimento na matemática por trabalharem a atenção, concentração,sequência, ritmo, organização espacial, temporal.
As brincadeiras “Escravos de Jó” e "Cinco Marias" são ótimos recursos para crianças com diagnóstico ou suspeita de Discalculia.
Escravos de Jó:
Coloque os alunos em roda, sentados no chão. Cada um deverá ter um objeto pequeno consigo – latinha de alumínio, caixa de fósforo, copos de plástico, entre outros. Assim que a música se inicia, os alunos deverão passar os objetos entre si, no tempo 1 de cada compasso. Você deve estabelecer em que sentido os objetos serão passados – horário ou anti-horário.
Após essa primeira rodada de “treinamento”, apresente à turma a brincadeira como é realizada tradicionalmente. Da mesma forma que há diferentes versões para a letra e para a melodia da música (ver os links disponibilizados em Recursos Complementares), outras versões para a forma de brincar e passar os objetos podem ser trazidas pelos alunos. Na medida do possível, tente executar as versões diferentes e, ao final, escolha junto a turma qual será realizada por todos.
Sugere-se algumas versões conhecidas:
1) A música inicia-se e os objetos são passados no tempo 1 de cada compasso. No trecho “Tira, bota”, os alunos devem levantar o objeto do chão e colocá-lo novamente, à sua frente, ainda no tempo 1 de cada compasso. No trecho seguinte “Deixa o Zé Pereira ficar”, os alunos devem pegar o objeto e batê-lo no chão, nos tempos 1 e 2 de cada compasso, até a frase terminar (coincidindo com o tempo 1 do compasso seguinte). A partir de “Guerreiros com guerreiros”, os objetos voltam a ser passados para o lado, no tempo 1 de cada compasso. No trecho “Zigue-zigue zá”, o objeto é passado para o lado na sílaba “zi” de “zigue”, retornado pelo mesmo aluno que passou na sílaba “zi”, da segunda palavra “zigue” e passado novamente, dessa vez de maneira efetiva, ao colega do lado. O movimento fica dessa forma, caso os objetos sejam passados no sentido anti-horário: direita – esquerda – direita.
2) A música inicia-se e os objetos são passados no tempo 1 de cada compasso. No trecho “Tira, bota”, os alunos devem levantar o objeto do chão e colocá-lo novamente, à sua frente, ainda no tempo 1 de cada compasso. No trecho seguinte “Deixa o Zé Pereira ficar”, os alunos devem fazer um gesto com as duas mãos, como se estivessem mandando o “Zé Pereira” embora, nos tempos 1 e 2 de cada compasso, até a frase terminar (coincidindo com o tempo 1 do compasso seguinte). A partir de “Guerreiros com guerreiros”, os objetos voltam a ser passados para o lado, no tempo 1 de cada compasso. No trecho “Zigue-zigue zá”, o objeto é passado para o lado na sílaba “zi” de “zigue”, retornado pelo mesmo aluno que passou na sílaba “zi”, da segunda palavra “zigue” e passado novamente, dessa vez de maneira efetiva, ao colega do lado. O movimento fica dessa forma, caso os objetos sejam passados no sentido anti-horário: direita – esquerda – direita.
Cinco-marias ou pipokinha:
Como pode ser chamado, é um jogo também conhecido como brincadeira dos cinco saquinhos (ou cinco pedrinhas, que devem ter tamanhos aproximados). Para brincar são necessários cinco saquinhos de tecido de mais ou menos 4 cm por 3 cm, com enchimento de areia, farinha, grãos de arroz ou feijão, ou as cinco pedrinhas.
As cinco-marias têm origem em um costume da Grécia antiga. Quando queriam consultar os deuses ou tirar a sorte, os homens jogavam ossinhos da pata de carneiro (astrágalos) e observavam como caíam.
Cada lado do ossinho tinha um nome e um valor, e a resposta divina às perguntas humanas era interpretada a partir da soma desses números. O lado mais liso era chamado kyon (valia 1 ponto), o menos liso, coos (6 pontos); o côncavo, yption (3 pontos), e o convexo, pranes (4 pontos).
Essa pode ser a origem dos dados (do latim, “dadus”, que quer dizer “dado pelos deuses”), segundo Renata Meirelles, autora do livro "Giramundo e outros brinquedos e brincadeiras dos meninos do Brasil".
Com o tempo, os ossinhos foram substituídos por pedrinhas, sementes e pedaços de telha até chegar aos saquinhos de tecido recheados com areia, grãos ou sementes, conta Meirelles.
- Jogar todos os saquinhos no chão (ou outra superfície) e pegar um deles sem tocar nos demais; jogar para o alto o saquinho escolhido, enquanto pega um dos outros quatro que estão no chão, e sem encostar nos restantes; segurar o saquinho na volta, com a mesma mão, antes que ele caia no chão; repetir o mesmo para cada um dos quatro saquinhos.
- Novamente, jogar os cinco saquinhos no chão e pegar um, sem tocar nos restantes; repetir a etapa anterior, só que agora de dois em dois saquinhos.
- Repetir tudo, mas desta vez pegando um saquinho e depois os três restantes ao mesmo tempo.
- Jogar os saquinhos, pegar um, jogá-lo para o alto, pegar os quatro saquinhos restantes de uma só vez e em seguida pegar o saquinho que estava no ar sem deixar cair nenhum.
- Na última etapa, jogar os cinco saquinhos no chão e pegar um sem tocar nos demais; com a outra mão, formar um túnel por onde os quatro saquinhos restantes deverão ser passados, um de cada vez, enquanto o saquinho escolhido estiver lançado ao ar.
Observação - Se o jogador tocar num dos saquinhos que estão no chão que não seja o escolhido para a execução da jogada ou deixar algum deles cair da mão, passará a vez para o próximo jogador.


Descrição das brincadeiras - Fonte:Wikipédia:
Fonte:
Rosangela L. S. Vali - Especialista em Psicopedagogia
Bibliografia:
CARRAHER, Terezinha Nunes (Org.). Aprender Pensando. Petrópolis, Vozes, 2002.
GARCÍA, J. N. Manual de Dificuldades de Aprendizagem. Porto Alegre, ArtMed, 1998.
JOSÉ, Elisabete da Assunção, Coelho, Maria Teresa. Problemas de aprendizagem. São Paulo, Ática, 2002.
RISÉRIO, Taya Soledad. Definição dos transtornos de aprendizagem. Programa de (re) habilitação cognitiva e novas tecnologias da inteligência. 2003.


 |
Sabe-se que a criança tem contato com o número mesmo antes de ingressar na escola: número da casa, idade, telefone, data de nascimento, etc. A partir dos primeiros contatos com a numeração dentro e fora da escola o estudante começa a estabelecer as primeiras hipóteses a respeito do processo de representação de quantidade, necessárias para compreender o Sistema de Numeração Decimal.
Neste post há algumas atividades para alfabetização que além de importantes, são pura diversão para a criançada.
• Inicialmente, é importante fazer explorações com cada número relacionando símbolo e quantidade: contar objetos, o próprio corpo.
• Contar objetos iguais: tampinhas, palitos, os dedos, os próprios alunos.
• Na construção do 3 já é possível fazer outras atividades como promover corridas e contar “1,2,3” para dar a largada. Esconder um brinquedo na sala e o aluno tem apenas 3 chances de encontrá-lo. Inventar uma história com três personagens.
• Em relação ao 4, já é possível explorar os veículos (quantas rodas?).
• A idéia do zero pode ser trabalhada através da subtração: tinha dois biscoitos, comi um, fiquei com um, comi outro e fiquei sem nada. (oralmente e manipulando objetos).
• Outra idéia importante é a de ponto de partida. “Se você está na linha de partida e ainda não se mexeu, quanto você andou?” (utilizar essa idéia em jogos, brincadeiras, etc.) A régua também é um ótimo material para perceber o zero com ponto de partida.• Sair da classe na hora do recreio e pedir que cada criança que saia diga um número em seqüência. (alternar a saída dos alunos em momentos diferentes para que todos possam perceber a seqüência numérica)
Começar a contar a partir de números maiores que 1.
• Brincadeiras cantadas:
“Um, dois, feijão com arroz
Três, quatro, feijão no prato
Cinco, seis, feijão japonês
Sete, oito, feijão com biscoito
Nove, dez, feijão com pastéis”
“A galinha do vizinho bota ovo amarelinho
Bota um, bota dois, bota três, bota quatro,
Bota cinco, bota seis, bota sete, bota oito,bota nove, bota dez!”
• Organizar com os alunos (eles devem fazer as construções dos materiais) bolinhas (ou similares) dentro de um saquinho transparente, marcar no saquinho o número referente à quantidade de bolinhas do saquinho. Pedir que a criança pegue, por exemplo, 5 bolinhas, ela poderá pegar o saquinho marcado com o número 5, ou o saquinho com 2 e 3, já trabalhando a ideia da subtração.
• Com os Blocos Lógicos:
a) Uma criança escolhe uma peça, e outras tentam tirar uma bem parecida.
b) Pedir as crianças por negação de atributo, uma peça que não seja azul.
c) Elaborar um cartaz, dividido em quatro partes, cada parte representa uma classe.
• Observar a fila que formam para, fazer brincadeiras colocando os alunos em fila sendo um menino e uma menina, por ordem de tamanho (do menor para o maior e vice-versa).
• Pedir às crianças que montem um colar ou um enfeite para sala com sucatas como: tampinhas, caixinhas, papéis, entre outros (em situações significativas: festa junina, apresentações, entre outras).
• Observar o calendário.
• Fábrica de fósforos: cada 6 palitos de fósforos serão colocados em uma caixa. A seguir, a cada 6 caixas completas serão colocadas em um saquinho de papel, ou seja a cada 6 elementos de um tipo trocamos por 1 elemento do tipo seguinte (palitos por caixa, caixas por saquinho). Após o fim da tarefa os alunos devem contar quem tem mais palitos. (variar a base)
• Sozinho, rodinha, corrente: os alunos devem formar grupos conforme o pedido do professor, por exemplo, suponhamos que haja 31 alunos. O professor pede grupos com 5 alunos, cada grupo formará uma rodinha, a cada grupo de 5 rodinhas teremos uma corrente. (variar a base)
• Resolva os problemas, desenhando em seguida. Use a linguagem matemática: Algumas crianças estavam brincando de mãe-pega: 5 já tinham sido pegas e 6 ainda estavam correndo. Quantas crianças estavam brincando?João estava jogando bafo com um amigo. Ele tinha 9 figurinhas e ao término do jogo estava somente com 5. Quantas figurinhas João perdeu para o amigo?
• Observando a régua quebrada (apresentar uma régua, quebrada no início e no final, que inicie a partir do 7 e vá até 30), responda as seguintes perguntas:
a) A régua está completa?
b) Que números estão faltando no início da régua?
c) Essa régua está quebrada no final e só mostra números até 25, mas ela vai até o 30.
d) Que números estão faltando no final?
• “Música da Dona Aranha” (cantar com os alunos).
a) O que a Dona Aranha poderia fazer para subir na parede e não cair mais por causa da chuva? (sugestão: usar tênis que não escorreguem)
b) Quantas patas tem uma aranha?
c) Quantos pares de tênis teríamos que arranjar para Dona Aranha?
d) Quantos tênis são?
• Para realização de um joguinho, é preciso dividir igualmente essas (12) fichas entre os (4) jogadores. Faça a divisão e responda:
a) Quantas fichas havia para dividir?
b) Quantas crianças receberam as fichas?
c) Quantas fichas cada criança recebeu?(atividade realizada com o material)
• Observe estas embalagens: pirulitos (10) e (35).
a) Quantas unidades há no pacote menor? E no maior?
b) Quantos pirulitos há dentro dessa embalagem? (10) Represente com desenhos.
c) E nesse pacote há quantos pirulitos?(35)4) Com esta quantidade forme grupos de dez.
d) Quantos grupos de 10 você formou?
e) Quanto pirulitos sobraram?
f) Quantos pirulitos há dentro da caixa?
• Observe estes pacotes: três pacotes com 10 pirulitos
a) Quantos pirulitos há em cada pacote?
b) Juntando os pirulitos dos três pacotes, quantos pacotes teríamos?
c) Quantos pacotes menores (com 10) seriam necessários para conseguir a quantidade de pirulitos do pacote maior (com 35) ?
d) Sobraram pirulitos? Quantos?
Dinheiro
a) Trabalhar com trocas, sempre manipulando o dinheiro (notas desenhadas): quantas notas de 1 real são necessárias para trocar por uma nota de 5 reais? E de 10 reais?
b) Trabalhar a situação inversa.
c) Atividades que envolvam compra, venda e troco.
Palitinhos e outros materiais
a) Trocas com os palitinhos utilizando bases diferentes.
b) Trocas com cartões coloridos.
c) Utilizar objetos diferentes: 3 palitos, trocar por uma tampinha, 3 tampinhas trocar por uma caixinha.
d) Trocas com os palitinhos na base 10 formando grupos e desfazendo-os.
e) Construir um cartaz de pregas individual para colocar os palitinhos (base 10).
Fonte: http://www.cidadedoconhecimento.org.br/cidadedoconhecimento/index.php?portal=480&con=1055





CORES...
DIVERSÃO!!!

O jogo contribui muito para desenvolver o raciocínio da criança.
No jogo com os dados de cores, quantidades e números e com as tampinhas de garrafa pet, as crianças tiveram a oportunidade de construir conhecimentos.



Qual a cor? qual a quantidade? quais tampinhas devo pegar?





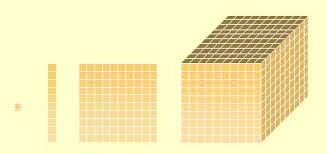
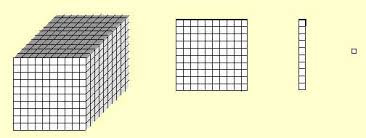
 Observe que o cubo é formado por 10 placas, que a placa é formada por 10 barras e a barra é formada por 10 cubinhos. Este material baseia-se em regras do nossso sistema de numeração.
Observe que o cubo é formado por 10 placas, que a placa é formada por 10 barras e a barra é formada por 10 cubinhos. Este material baseia-se em regras do nossso sistema de numeração.
 Veja como representamos, com ele, o número 265:
Veja como representamos, com ele, o número 265:
 Este material pedagógico, confeccionado em madeira, costuma ser comercializado com o nome de material dourado. Você pode construir um material semelhante, usando cartolina. Os cubinhos são substituídos por quadradinhos de lado igual a 2 cm, por exemplo. As barrinhas são substituídas por retângulos de 2 cm por 20 cm a as placas são substituídas por quadrados de lado igual a 20 cm.
Este material pedagógico, confeccionado em madeira, costuma ser comercializado com o nome de material dourado. Você pode construir um material semelhante, usando cartolina. Os cubinhos são substituídos por quadradinhos de lado igual a 2 cm, por exemplo. As barrinhas são substituídas por retângulos de 2 cm por 20 cm a as placas são substituídas por quadrados de lado igual a 20 cm.


O jogo contribui muito para desenvolver o raciocínio da criança.
No jogo com os dados de cores, quantidades e números e com as tampinhas de garrafa pet, as crianças tiveram a oportunidade de construir conhecimentos.



Qual a cor? qual a quantidade? quais tampinhas devo pegar?



Construindo sequências!
O Material Dourado Montessori destina-se a atividades que auxiliam o ensino e a aprendizagem do sistema de numeração decimal-posicional e dos métodos para efetuar as operações fundamentais (ou seja, os algoritmos).No ensino tradicional, as crianças acabam "dominando" os algoritmos a partir de treinos cansativos, mas sem conseguirem compreender o que fazem. Com o Material Dourado a situação é outra: as relações numéricas abstratas passam a ter uma imagem concreta, facilitando a compreensão. Obtém-se, então, além da compreensão dos algoritmos, um notável desenvolvimento do raciocínio e um aprendizado bem mais agradável.O Material Dourado faz parte de um conjunto de materiais idealizados pela médica e educadora italiana Maria Montessori.
Vamos conhecer o material das contas pelas palavras de Maria Montessori:
"Preparei também, para os maiorezinhos do curso elementar, um material destinado a representar os números sob forma geométrica. Trata-se do excelente material denominado material das contas. As unidades são representadas por pequenas contas amarelas; a dezena (ou número 10) é formada por uma barra de dez contas enfiadas num arame bem duro. Esta barra é repetida 10 vezes em dez outras outras barras ligadas entre si, formando um quadrado, "o quadrado de dez", somando o total de cem. Finalmente, dez quadrados sobrepostos e ligados formando um cubo, "o cubo de 10", isto é, 1000.Aconteceu de crianças de quatro anos de idade ficarem atraídas por esses objetos brilhantes e facilmente manejáveis. Para surpresa nossa, puseram-se a combiná-los, imitando as crianças maiores. Surgiu assim um tal entusiasmo pelo trabalho com os números, particularmente com o sistema decimal, que se pôde afirmar que os exercícios de aritmética tinham se tornado apaixonantes.As crianças foram compondo números até 1000. O desenvolvimento ulterior foi maravilhoso, a tal ponto que houve crianças de cinco anos que fizeram as quatro operações com números de milhares de unidades".
Essas contas douradas acabaram se transformando em cubos que hoje formam o Material Dourado Montessori.
O Material Dourado ou Montessori é constituído por cubinhos, barras, placas e cubão, que representam:
Embora seja possível representar o milhar, vamos evitá-lo trabalhando com números menores.
Damos a seguir sugestões para o uso do Material Dourado Montessori.
As atividades propostas foram testadas e mostraram-se eficazes desde o segundo ano até o quinto ano. Muitas delas foram concebidas pelos grupos de alunos, recomendando-se que os grupos não tenham mais do que 6 alunos.O professor, com o conhecimento que tem de seus alunos, saberá em que ano cada atividade poderá ser aplicada com melhor rendimento. Várias das atividades podem ser aplicadas em todos os anos iniciais, bastando, para isso, pequenas modificações.Utilizando o material, o professor notará em seus alunos um significativo avanço de aprendizagem.
Atividades para Aplicação e Compreensão da Composição,
Decomposição de Números e Operações Matemáticas
1. JOGOS LIVRES
Objetivo: tomar contato com o material, de maneira livre, sem regras.
Durante algum tempo, os alunos brincam com o material, fazendo construções livres.
O material dourado é construído de maneira a representar um sistema de agrupamento. Sendo assim, muitas vezes as crianças descobrem sozinhas relações entre as peças. Por exemplo, podemos encontrar alunos que concluem:
- Ah! A barra é formada por 10 cubinhos!
- E a placa é formada por 10 barras!
- Veja, o cubo é formado por 10 placas!
2. MONTAGEM
Objetivo: perceber as relações que há entre as peças.
O professor sugere as seguintes montagens:
- uma barra;
- uma placa feita de barras;
- uma placa feita de cubinhos;
- um bloco feito de barras;
- um bloco feito de placas;
O professor estimula os alunos a obterem conclusões com perguntas como estas:
- Quantos cubinhos vão formar uma barra?
- E quantos formarão uma placa?
- Quantas barras preciso para formar uma placa?
Nesta atividade também é possível explorar conceitos geométricos, propondo desafios como estes:
- Vamos ver quem consegue montar um cubo com 8 cubinhos? É possível?
- E com 27? É possível?
3. DITADO
Objetivo: relacionar cada grupo de peças ao seu valor numérico.
O professor mostra, um de cada vez, cartões com números. As crianças devem mostrar as peças correspondentes, utilizando a menor quantidade delas.
O professor mostra peças, uma de cada vez, e os alunos escrevem a quantidade correspondente.
4. FAZENDO TROCAS
Objetivo: compreender as características do sistema decimal.
- fazer agrupamentos de 10 em 10;
- fazer reagrupamentos;
- fazer trocas;
- estimular o cálculo mental.
Para esta atividade, cada grupo deve ter um dado marcado de 4 a 9.
Cada criança do grupo, na sua vez de jogar, lança o dado e retira para si a quantidade de cubinhos correspondente ao número que sair no dado.Veja bem: o número que sai no dado dá direito a retirar somente cubinhos.Toda vez que uma criança juntar 10 cubinhos, ela deve trocar os 10 cubinhos por uma barra. E aí ela tem direito de jogar novamente.Da mesma meneira, quando tiver 10 barrinhas, pode trocar as 10 barrinhas por uma placa e então jogar novamente.O jogo termina, por exemplo, quando algum aluno consegue formar duas placas.
O professor então pergunta:
- Quem ganhou o jogo?
- Por quê?
Se houver dúvida, fazer as "destrocas".O objetivo do jogo das trocas é a compreensão dos agrupamentos de dez em dez (dez unidades formam uma dezena, dez dezenas formam uma centena, etc.), característicos do sistema decimal.A compreensão dos agrupamentos na base 10 é muito importante para o real entendimento das técnicas operatórias das operações fundamentais.O fato de a troca ser premiada com o direito de jogar novamente aumenta a atenção da criança no jogo. Ao mesmo tempo, estimula seu cálculo mental. Ela começa a calcular mentalmente quanto falta para juntar 10, ou seja, quanto falta para que ela consiga fazer uma nova troca.
cada placa será destrocada por 10 barras;
cada barra será destrocada por 10 cubinhos.
Variações:Pode-se jogar com dois dados e o aluno pega tantos cubinhos quanto for a soma dos números que tirar dos dados.Pode-se utilizar também uma roleta indicando de 1 a 9.
5. PREENCHENDO TABELAS
Objetivo: os mesmos das atividades 3 e 4.
- preencher tabelas respeitando o valor posicional;
- fazer comparações de números;
- fazer ordenação de números.
As regras são as mesmas da atividade 4. Na apuração, cada criança escreve em uma tabela a quantidade conseguida.
Olhando a tabela, devem responder perguntas como estas:
- Quem conseguiu a peça de maior valor?
- E de menor valor?
- Quantas barras Lucilia tem a mais que Gláucia?Olhando a tabela à procura do vencedor, a criança compara os números e percebe o valor posicional de cada algarismo.Por exemplo: na posição das dezenas, o 2 vale 20; na posição das centenas vale 200.Ao tentar determinar os demais colocados (segundo, terceiro e quarto lugares) a criança começa a ordenar os números.
6. PARTINDO DE CUBINHOS
Objetivo: os mesmos da atividade 3, 4 e 5.
Cada criança recebe um certo número de cubinhos para trocar por barras e depois por placas.A seguir deve escrever na tabela os números correspondentes às quantidades de placas, barras e cubinhos obtidos após as trocas.Esta atividade torna-se interessante na medida em que se aumenta o número de cubinhos.
7. VAMOS FAZER UM TREM?
Objetivo: compreender que o sucessor é o que tem "1 a mais" na seqüência numérica.
O professor combina com os alunos:
- Vamos fazer um trem. O primeiro vagão é um cubinho. O vagão seguinte terá um cubinho a mais que o anterior e assim por diante. O último vagão será formado por duas barras.
8. UM TREM ESPECIAL
Objetivo: compreender que o antecessor é o que tem "1 a menos" na seqüência numérica.
O professor combina com os alunos:
- Vamos fazer um trem especial. O primeiro vagão é formado por duas barras (desenha as barras na lousa). O vagão seguinte tem um cubo a menos e assim por diante. O último vagão será um cubinho.
9. JOGO DOS CARTÕES
Objetivos: compreender o mecanismo do "vai um" nas adições; estimular o cálculo mental.
O professor coloca no centro do grupo alguns cartões virados para baixo. Nestes cartões estão escritos números entre 50 e 70.1º sorteio: Um alunos do grupo sorteia um cartão. Os demais devem pegar as peças correspondentes ao número sorteado.Em seguida, um representante do grupo vai à lousa e registra em uma tabela os números correspondentes às quantidades de peças.2º sorteio: Um outro aluno sorteia um segundo cartão. Os demais devem pegar as peças correspondentes a esse segundo número sorteado.Em seguida, o representante do grupo vai à tabela registrar a nova quantidade.Nesse ponto, juntam-se as duas quantidades de peças, fazem-se as trocas e novamente completa-se a tabela.Ela pode ficar assim:
Isto encerra uma rodada e vence o grupo que tiver conseguido maior total. Depois são feitas mais algumas rodadas e o vencedor do dia é o grupo que mais rodadas venceu.Os números dos cartões podem ser outros. Por exemplo, números entre 10 e 30, na primeira série; entre 145 e 165, na segunda série.Depois que os alunos estiverem realizando as trocas e os registros com desenvoltura, o professor pode apresentar a técnica do "vai um" a partir de uma adição como, por exemplo, 15 + 16.Observe que somar 15 com 16 corresponde a juntar estes conjuntos de peças.
Fazendo as trocas necessárias,
Compare, agora, a operação:
com o material
com os números
Ao aplicar o "vai um", o professor pode concretizar cada passagem do cálculo usando o material ou desenhos do material, como os que mostramos.
O "vai um" também pode indicar a troca de 10 dezenas por uma centena, ou 10 centenas por 1 milhar, etc.
Veja um exemplo:
No exemplo que acabamos de ver, o "vai um" indicou a troca de 10 dezenas por uma centena.É importante que a criança perceba a relação entre sua ação com o material e os passos efetuados na operação.
10. O JOGO DE RETIRAR
Objetivos: compreender o mecanismo do "empresta um" nas subtrações com recurso; estimular o cálculo mental.
Esta atividade pode ser realizada como um jogo de várias rodadas. Em cada rodada, os grupos sorteiam um cartão e uma papeleta. No cartão há um número e eles devem pegar as peças correspondentes a essa quantia. Na papeleta há uma ordem que indica quanto devem tirar da quantidade que têm.
Por exemplo: cartão com número 41 e papeleta com a ordem: TIRE 28.
Vence a rodada o grupo que ficar com as peças que representam o menor número. Vence o jogo o grupo que ganhar mais rodadas.É importante que, primeiro, a criança faça várias atividades do tipo: "retire um tanto", só com o material. Depois que ela dominar o processo de "destroca", pode-se propor que registre o que acontece no jogo em uma tabela na lousa.Isto irá proporcionar melhor entendimento do "empresta um" na subtração com recurso. Quando o professor apresentar essa técnica, poderá concretizar os passos do cálculo com auxílio do material ou desenhos do material.O "empresta um" também pode indicar a "destroca" de uma centena por 10 dezenas ou um milhar por 10 centenas, etc. Veja o jogo seguinte:
11. "DESTROCA"
Objetivos: os mesmos da atividade 10.
Cada grupo de alunos recebe um dado marcado de 4 a 9 e uma placa.Quando o jogador começa, todos os participantes têm à sua frente uma placa.Cada criança, na sua vez de jogar, lança o dado e faz as "destrocas" para retirar a quantidade de cubinhos correspondente ao número que sair no dado. Veja bem: esse número dá direito a retirar somente cubinhos.Na quarta rodada, vence quem ficar com as peças que representam o menor número.Exemplo: Suponha que um aluno tenha tirado 7 no dado. Primeiro ele troca uma placa por 10 barras e uma barra por 10 cubinhos:
Depois, retira 7 cubinhos:
Salienta-se novamente a importância de se proporem várias atividades como essa, utilizando, de início, só o material. Quando o processo de "destroca" estiver dominado, pode-se propor que as crianças façam as subtrações envolvidas também com números.
Atividades para Impressão,Recorte e Colagem de Atividades e Registros Diversos:





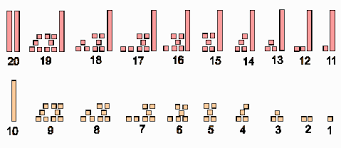

Atividades para Impressão,Recorte e Colagem de Atividades e Registros Diversos:








































